ThomasFriday.com | A fascinating method to draw fractals

You've probably heard about fractals before. They are geometric shapes that repeat themselves over and over again. I recently discovered a fascinating method to draw them that is called "chaos game".

Anyone can draw impressive looking fractals with this method, even with just a pen and paper. In this article I will describe the method, share my JavaScript code to generate them, and show many examples of fractals made with it.

The algorithm

The chaos game algorithm is quite simple. We start with a geometric shape (triangle, rectangle, ...) and follow these steps:

Pick a random point within the shape. Let's call it p.
Pick a random corner of the shape. Let's call it c.
Compute the coordinates midway between p and c.
Call this new point p, and draw it.
Go back to step 2.

Here's an example of how this would look like in a triangle.

If we repeat these steps a few thousands times, we end up with this.

Pretty cool! That's a fractal called the Sierpinski triangle.

How it works

I was surpised that such a simple algorithm could produce the image above. Let's try to understand why this works.

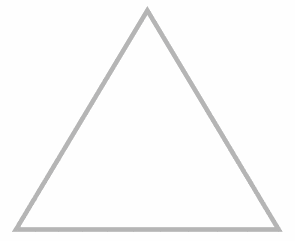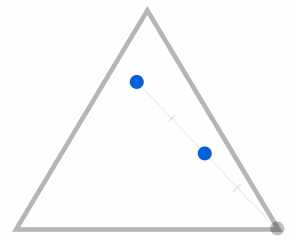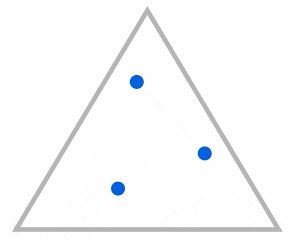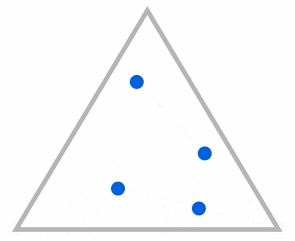
If we pick a few random points within the triangle, and move them toward the top corner as explained by the algorithm, this happens.

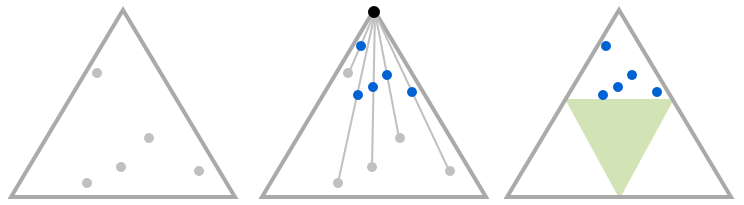
We can see that none of the resulting points (in blue) end up in the middle triangle (in green). So this area will always stay empty.

Now we try the same thing with one change: we won't put any points in the green triangle since we know they can't end up here.

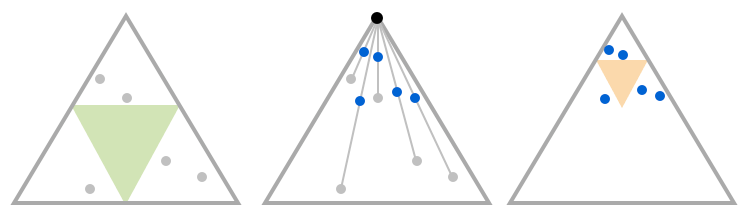
This time there are no points in the smaller top triangle (in orange). This means that this area will also stay empty.

The same process repeats itself towards infinity and works with the three corners. In the end this produces the Sierpinski triangle.

The code

We will soon see many other examples of fractals, but first here's the code I'm using to draw them with HTML and JavaScript.

We start by creating a basic HTML page that contains a <canvas> element followed by a script tag.

<!DOCTYPE html>
<html>
  <head>
    <meta charset="UTF-8">
    <title>Fractals</title>
  </head>
  <body>
    <canvas width="500" width="500" id="canvas"></canvas>
    <script>
        /* Add JavaScript code here */
    </script>
  </body>
</html>

Inside the script tag we write this JavaScript code that follows the chaos game algorithm. I added a lot of comments to explain what is going on.

// Variables needed to draw on the canvas
const canvas = document.getElementById('canvas');
const ctx = canvas.getContext('2d');

// Coordinates of the shape's points 
const shape = [
  { x: 250, y: 0 },
  { x: 500, y: 400 },
  { x: 0, y: 400 },
];

// Coordinates of a random point
let point = {
  x: Math.round(Math.random() * 500),
  y: Math.round(Math.random() * 500),
};

// How many points we've drawn so far
let count = 0;

while (count < 15000) {
  // Pick a random number: 0, 1, or 2
  let rand = Math.floor(Math.random() * shape.length);

  // Select a corner based on the random number
  let corner = shape[rand];

  // Compute coordinates, midway between 'point' and 'corner'
  point.x = (point.x + corner.x) / 2;
  point.y = (point.y + corner.y) / 2;

  // Draw the new point
  ctx.fillRect(point.x, point.y, 1, 1);

  // Increment 'count', once it reaches 15000 we stop the loop
  count++;
}

Square, version 1

Let's try to replace the triangle by a square and keep everything else the same.

const shape = [
  { x: 0, y: 0 },
  { x: 0, y: 500 },
  { x: 500, y: 500 },
  { x: 500, y: 0 },
];

When we open our HTML file in a browser, we get this result.

That's a little disappointing, it's just random points in a square. But wait, we can do better.

Square, version 2

We make a small change to the while loop, so that we never pick the same corner twice in a row.

// New variable 
let previousRand = null;

while (count < 15000) {
  // Pick a random number
  let currentRand = Math.floor(Math.random() * shape.length);

  // If it's different from the previous one we picked
  if (currentRand !== previousRand) {
    // Update the previousRand variable
    previousRand = currentRand; 

    // Same as before
    let corner = shape[currentRand];
    point.x = (point.x + corner.x) / 2;
    point.y = (point.y + corner.y) / 2;
    ctx.fillRect(point.x, point.y, 1, 1);
    count++;
  }
}

This new code produces a beautiful fractal.

More squares

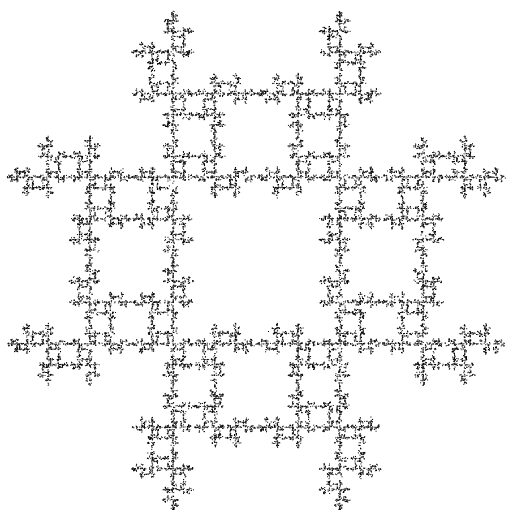
With slightly different conditions in the loop, it's possible to create completely new fractals with our square. Below are some interesting examples.

Here's what happens when currentRand can't be one spot away from previousRand anti-clockwise.

if ((previousRand + 1) % 4 !== currentRand)

This is when currentRand can't be opposite to previousRand.

if ((previousRand + 2) % 4 !== currentRand)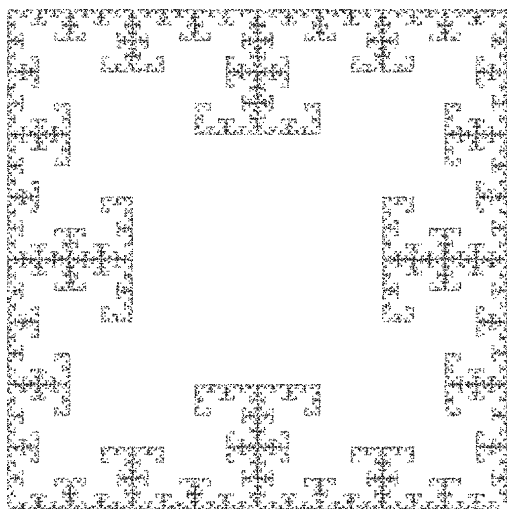

And if we also store the previousPreviousRand, we can do things like this.

if ((previousRand + 3) % 4 !== currentRand && 
    (perviousPreviousRand + 1) % 4 !== currentRand)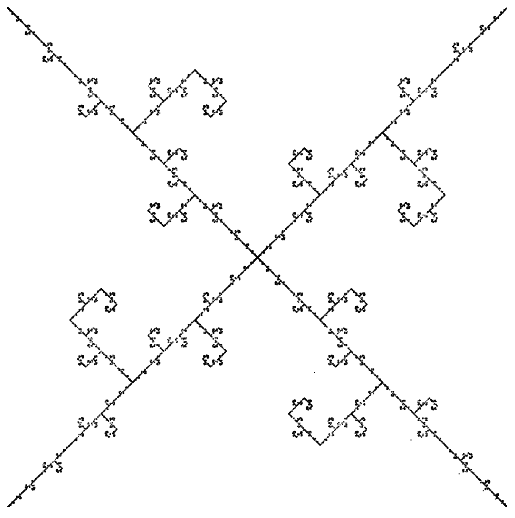

Pentagon

What worked with a triangle and a square will also work with many other shapes. Here's a cool looking example with a pentagon.

Conclusion

I find it fascinating that a simple algorithm can generate many complex and cool looking shapes.